Mist – Lagerschaden! Wenn ihr bedenkt, dass Wälzlager einer anhaltenden Druck- und Scherbelastung ausgesetzt sind, ist dies zunächst einmal nichts Ungewöhnliches. Entscheidend ist dabei eher der Zeitpunkt des Lagerausfalls. Zur Dimensionierung einer Lagerstelle und damit der Lagerausfall nicht zu überraschend kommt bzw. man ihm vorbeugen kann, ist die Berechnung der Lebensdauer von zentraler Bedeutung. Dabei wird das Leben eines Lagers nicht in Jahren, sondern mit der Gesamtzahl der Umdrehungen oder Betriebsstunden angegeben, die bis zum Eintritt eines natürlichen Ermüdungsschadens des Materials theoretisch möglich sind.
Die nominelle Lebensdauer L10
Die wohl bekannteste Wälzlagerlagerlebensdauer, welche oft auch „Kataloglebensdauer“ genannt wird, wird mit L10 bezeichnet und ist nach DIN 281:2007 genormt (Berechnungsformel siehe unten). Voraussetzung für das Erreichen der rechnerischen Lebensdauer sind realistische Einschätzungen der Betriebszustände wie Drehzahl, Belastung und Umgebungsbedingungen.
| L10 | Nominelle Lebensdauer in 106 Umdrehungen | |||
| L10h | Nominelle Lebensdauer in Betriebsstunden | |||
| C | Dynamische Tragzahl laut Tabelle (siehe z.B. NTN Katalog (Cr: Radiallager, Ca: Axiallager) | |||
| P | Dynamisch äquivalente Belastung (Pr: Radiallager, Pa: Axiallager) | |||
| p | Lebensdauerexponent (Kugellager: p = 3, Rollenlager: p = 10/3) | |||
| n | Drehzahl des Wälzlagers in der Anwendung, min-1 | |||
Da sich Wälzlager aufgrund von Fertigungstoleranzen und Werkstoffbeschaffenheiten geringfügig voneinander unterscheiden, weisen eine Gruppe von Lagern des gleichen Typs unter denselben Betriebsbedingungen (gleiche Drehzahl, Belastung und Schmierung) in der Realität eine variierende Lebensdauer auf. Dieser sogenannte Streubereich gleicht dabei einer Wahrscheinlichkeitsangabe, da er statistisch ermittelt wird. Anhand der statistischen Lebensdauer (der nominellen Lebensdauer L10 nach DIN ISO 281:2007) wird die Gesamtzahl der Umdrehungen in Millionen angegeben, die von 90 % aller Lager in einer baugleichen Gruppe erreicht wird, bis eine Materialermüdung auftritt. Dies gilt unter identischen Betriebszuständen bei einer konstanten Drehzahl.
Auf die Frage „warum denn nur 90 %?“ gibt es eine simple Antwort: Der Grund ist, dass der Betrieb einer Anlage mit 100%iger Erfüllung der berechneten Lebensdauer zumeist schlicht zu teuer ist. Der Streubereich von 90 % bedeutet zugleich, dass die anderen 10 % vor dem angegebenen Zeitpunkt ausfallen „dürfen“. Dabei unterscheidet sich die Berechnung von L10 durch den Exponenten – abhängig davon, ob die Lebensdauer eines Kugellagers oder eines Rollenlagers berechnet wird. Mit Hilfe der nominellen Lebensdauer L10h wird dabei die Anzahl der erreichbaren Betriebsstunden angegeben (Formel 1).
Formel 1
Lebensdauer in 106 Umdrehungen:
für Kugellager: L10 = (C/P)3
für Rollenlager: L10 = (C/P)10/3
Lebensdauer in Betriebsstunden:
L10h = (16 666,6 ̅/n) x (C/P)p
Für Kugellager gilt: Wenn man die Last halbiert oder die Tragzahl verdoppelt, verachtfacht man die Lebensdauer.
Höchste Lebensdaueranforderungen an Wälzlager werden übrigens insbesondere in der Windkraft sowie bei E-Motoren und Werkzeugmaschinen gestellt. Bei Anwendungen aus der Landwirtschaft, in der einige Maschinen nur saisonal zum Einsatz kommen, wird dagegen eine geringere Lebensdauer rechnerisch gefordert – hier spielen Verschmutzung und andere ungünstige Umgebungsbedingungen zudem eine große Rolle, welche rechnerisch nicht immer abgebildet werden können.
Die nominelle Lebensdauer in Stunden L10h
Eine wichtige Grundlage für die Berechnung von L10h bildet die lagerspezifisch dynamische Tragzahl C , die das Tragvermögen von Wälzlagern und demzufolge die dynamische Last, die ein Lager tragen kann, angibt. Die Berechnung der dynamischen Tragzahl ist ebenfalls nach DIN 281:2007 genormt und wird für Standardlager vom Wälzlagerhersteller im jeweiligen Katalog angegeben. Bei einer Belastung des Wälzlagers in Höhe der dynamischen Tragzahl erreicht das Lager rechnerisch eine Lebensdauer von 1 Mio. Umdrehungen. In der Praxis sollten hier aber noch weitere Bedingungen eingehalten bzw. überprüft werden… Bei Radiallagern wird übrigens ausschließlich die radiale und bei Axiallagern nur die axiale Belastungsrichtung in der dynamischen Tragzahl angegeben. Aus diesem Grund wird zwischen den Bezeichnungen Cr für Radiallager und Ca für Axiallager differenziert.
Bei vielen Lagerungen greift die Last F in einem Winkel am Wälzlager an. Hieraus resultieren dann eine Radialkraft Fr und eine Axialkraft Fa. Zur Berechnung der nominellen Lebensdauer wird jedoch eine Belastung konstanter Größe und Richtung vorausgesetzt. Daher wird aus den beiden Kräften die äquivalente dynamische Lagerbelastung bestimmt, welche bei Radiallagern als äquivalente dynamische radiale Belastung (Pr) und bei Axiallagern als äquivalente dynamische axiale Belastung (Pa) bezeichnet wird. Bei der Belastung des Lagers mit dieser rechnerisch ermittelten Ersatzbelastung erzielt das Wälzlager die gleiche L10 -Lebensdauer wie bei den tatsächlich vorliegenden Lastverhältnissen.
Zudem müssen Wälzlager mit einer Mindestbelastung betrieben werden, um ein sicheres Abrollen der Wälzkörper zu gewährleisten und Gleitanteile zu minimieren. Letztere sollten dringend vermieden werden, um Anschmierungen (also die Bildung von Materialaufwürfen und die Entstehung einer rauen Laufbahnoberfläche) zu unterbinden, da diese zu einem frühzeitigen Lagerausfall führen können. Die empfohlene Mindestbelastung ist je nach Wälzlagerart unterschiedlich und sollte zum Beispiel bei Pendelrollenlagern 0,01 x C0 betragen.
Bereits festgelegt ist der Lebensdauerexponent p, eine Formel benötigt man somit nicht. Das Einzige, was beachtet werden muss, ist, um welche Bauform es sich bei dem Wälzlager handelt, dessen Lebensdauer berechnet werden soll. Demnach besitzt der Lebensdauerexponent bei Kugellagern einen Wert von p = 3, während dieser bei Rollenlagern p = 10/3 beträgt.
Beispielrechnung von L10 und L10h
Lager: 6206C3
Cr = 21,6 kN
Fa = 250 N
Fr = 2 000 N
n = 2000 U/min
X = 1, Y = 0, da Fa/Fr ≤ e
Pr = 2 kN
L10 = (21,6/2)3 = 1 259,71 x 106 Umdrehungen
L10h = 10 497,6 h
Die Berechnung von L10 und L10h am Beispiel des Rillenkugellagers 6206C3.
Die erweiterte modifizierte Lebensdauer Lnm bzw. Lnmh
Obwohl der Streubereich der nominellen Lebensdauer L10 standardmäßig auf einen Zuverlässigkeitsbeiwert von 90 % ausgerichtet ist, gibt es bestimmte Anwendungsbereiche, in denen dieser höher sein muss. Daraufhin kommt die erweiterte und ebenfalls nach DIN ISO 281:2007 genormte Lebensdauer Lnm bzw. Lnmh ins Spiel, um die man bei der Lebensdauerberechnung in einigen Fällen nicht herumkommt.
Formel 3
Lnm = a1 x aISO x L10
Lnmh = a1 x aISO x L10h
| Lnm | Erweiterte Lebensdauer in 106 Umdrehungen |
| Lnmh | Erweiterte Lebensdauer in Stunden |
| a1 | Lebensdauerbeiwert für die Zuverlässigkeit |
| aISO | Lebensdauerbeiwert für die Betriebsbedingungen aISO = f (ec × Cu ÷ P, κ) ec = Verunreinigungsbeiwert Cu = Ermüdungsgrenzbelastung P = dynamisch äquivalente Belastung κ = Viskositätsverhältnis |
| L10 | Nominelle Lebensdauer: Bezugslebensdauer in 106 Umdrehungen |
Kein Trick, sondern simple Mathematik: die modifizierte Berechnung der Wälzlagerlebensdauer Lnm und Lnmh . Allerdings muss man zuvor insbesondere für aISO einiges berechnen.
Die praktische Erfahrung zeigt, dass Wälzlager bei idealen Betriebsbedingungen durchaus die nach L10 berechneten Werte übertreffen können. Ein Beispiel wäre ein tragender Schmierfilm zwischen den Wälzkörpern und Ringen ohne Verschmutzungen und Verunreinigungen. Bemerkenswert ist, dass sogar sehr hohe Lebensdauern bis in den dauerfesten Bereich möglich sind. Voraussetzungen dafür sind dabei optimale Betriebsbedingungen und eine geringe Lagerbelastung. Bei einer maximalen Kontaktspannung von 1500 MPa wird das Lager in der Regel als dauerfest bezeichnet (Lagerbelastung unterhalb der Grenzbelastung Cu). Die erweiterte modifizierte Lebensdauer liefert dementsprechend genauere und eventuell auch realitätsnähere Ergebnisse als die nominelle Lebensdauer.
Für a1 wird grundsätzlich eine Ausfallwahrscheinlichkeit von 10 % vorausgesetzt. Aus diesem Grund entspricht a1 = 1 und somit verändert sich der Wert von a1 bei einer anderen Ausfallwahrscheinlichkeit dementsprechend.
| Zuverlässigkeit | Ln | Zuverlässigkeitsbeiwert a1 |
| 90 % | L10 | 1,00 |
| 95 % | L5 | 0,62 |
| 96 % | L4 | 0,53 |
| 97 % | L3 | 0,44 |
| 98 % | L2 | 0,33 |
| 99 % | L1 | 0,21 |
Der Zuverlässigkeitsbeiwert a1 sinkt bei höherer prozentualer Zuverlässigkeit der Lebensdauerangabe.
Der Faktor aISO stellt eine Funktion basierend auf der Schmierung, der Verunreinigung, den Materialeigenschaften sowie der Belastung dar und kann durch die folgende Formel beschrieben werden:
Verunreinigungen durch harte Partikel im Schmierstoff können zu Vertiefungen auf der Laufbahnoberfläche führen, die in oberflächenbedingten Schäden und einer Verkürzung der Lagerlebensdauer resultieren. Der Verunreinigungsbeiwert eC berücksichtigt dies und hängt vom Verschmutzungsgrad, der Lagergröße und der Schmierstoffviskosität (Schmierfilmdicke) ab.
| Verunreinigungsgrad | ec | |
Dpw < 100 mm | Dpw ≥ 100 mm | |
Höchste Sauberkeit Partikelgröße in Größenordnung der Schmierfilmdicke; Laborbedingungen | 1 | 1 |
Hohe Sauberkeit Öl durch extrem feinen Filter gefiltert; Bedingungen, die für lebensdauergeschmierte Lager mit Dichtscheiben typisch sind | 0,8 ~ 0,6 | 0,9 ~ 0,8 |
Normale Sauberkeit Öl durch feinen Filter gefiltert, Bedingungen, die für lebensdauergeschmierte Lager mit Deckscheiben typisch sind | 0,6 ~ 0,5 | 0,8 ~ 0,6 |
Leichte Verunreinigung Leichte Verunreinigung des Schmierstoffs | 0,5 ~ 0,3 | 0,6 ~ 0,4 |
Typische Verunreinigung Typische Bedingungen bei Lagern ohne integrierte Dichtungen; grobe Filterung; Verschleißpartikel und Kontamination aus der Umgebung | 0,3 ~ 0,1 | 0,4 ~ 0,2 |
Starke Verunreinigung Lagerumgebung stark verunreinigt und Lageranordnung mit unzureichender Abdichtung | 0,1 ~ 0 | 0,1 ~ 0 |
| Sehr starke Verunreinigung | 0 | 0 |
Die Ermüdungsgrenzbelastung stellt eine weitere Einflussgröße dar und ist die Last, die auf ein Lager ausgeübt wird und zur Ermüdungsgrenzspannung am höchstbelasteten Kontakt innerhalb der Laufbahn führt. Dies hängt vom Lagertyp, den internen Spezifikationen, der Qualität und der Materialfestigkeit ab. In ISO 281:2007 werden 1,5 GPa als Kontaktspannung entsprechend Cu für die Lager empfohlen, die aus üblicherweise verwendetem hochwertigem Material und guter Fertigungsqualität bestehen.
Ferner wird in aISO das Viskositätsverhältnis κ integriert, das den Einfluss der Schmierfilmbildung beschreibt. Lager werden unter der Annahme verwendet, dass die Wälzkontaktfläche durch einen Schmierfilm getrennt ist. Wenn jedoch die Viskosität des Schmierstoffs niedrig ist, wird die Trennung unzureichend und es tritt ein Festkörperkontakt auf, was zu einer Beschädigung führt. Das Viskositätsverhältnis κ berücksichtigt diesen Effekt und wird durch die unten angegebene Formel und durch das Verhältnis der Betriebsviskosität v zur Bezugsviskosität v1 beschrieben.
Formel 4
κ = v/v1
Die Berechnung des Viskositätsverhältnisses κ.
Formel 5
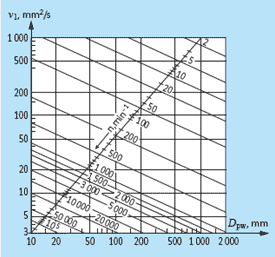
Falls n < 1 000 min-1, v1 = 45 000 n-0,83 Dpw-0,5
Falls n ≥ 1 000 min-1, v1 = 4 500 n-0,5 Dpw-0,5
Die Bezugsviskosität v1 hängt von der Drehzahl n und der Größe Dpw ab.
In den abgebildeten Diagrammen ist die Beziehung zwischen Cu/P, ec, κ und aISO von verschiedenen Lagertypen dargestellt. Die Verwendung der Abbildung unterliegt den Einschränkungen, dass der Lebensdauerbeiwert auf aISO ≤ 50 begrenzt ist und bei κ > 4 der Wert von κ = 4 anzunehmen ist. Der Ansatz ist zudem nicht gültig für κ < 0,1.
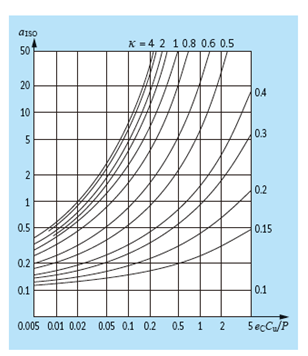

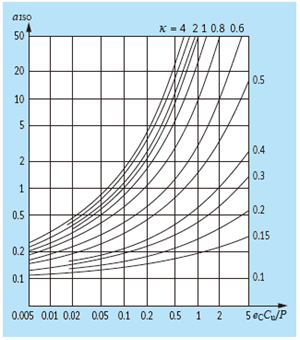
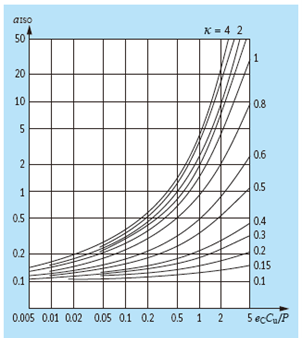
In den Abbildungen sind Angaben zum Lebensdauerbeiwert aISO von (v. l. n. r.) Radialkugellagern, Radialrollenlagern, Axialkugellagern und Axialrollenlagern vorhanden.
Beispielrechnung von L10mh
Gleiches Lager und Anwendung wie oben: 6206C3
Cr = 21,6 kN
Cu = 0,795 kN
Fa = 250 N
Fr = 2 000 N
n = 2 000 U/min
Hohe Sauberkeit der Umgebung
Schmierstoffviskosität bei Betriebstemperatur 80 °C von 14,37 mm²/s
X = 1, Y = 0, da Fa/Fr ≤ e
Pr = 2 kN
L10 = (21,6/2)3 = 1 259,71 x 106 Umdrehungen
L10h = 10 497,6 h
Mit Dpw < 100 mm folgt eC = 0,6 – 0,8
Mit Formel 5 folgt für v1 = 14,76 mm²/s
Daraus folgt κ = 0,9
Aus dem Diagramm für Radialkugellager kann für aISO ein Wert von ca. 8 abgelesen werden
Daraus folgt für L10hm = 83 981 h
Die Berechnung von L10mh am Beispiel des Rillenkugellagers 6206C3.
Weitere Methoden zur Berechnung der Lagerlebensdauer
Neben den hier dargestellten Verfahren zur Bestimmung der Lebensdauer eines Wälzlagers existieren noch weitere Methoden zur Berechnung hinsichtlich eines Ausfalls durch Materialermüdung. So wird bei der Berechnung der Referenzlebensdauer nach ISO TS 16281 die Lastverteilung des Wälzkörpers über seine Länge anhand eines Scheibchenmodells betrachtet. Bei diesem Verfahren werden weitere Einflussgrößen wie das Betriebsspiel und die Verkippung des Lagers, aber auch die vorliegenden Kontaktspannungen der jeweiligen Wälzkontakte berücksichtigt. Aufgrund des immensen Rechenaufwands eignet sich so ein Verfahren jedoch nur bei der Verwendung eines Berechnungsprogramms.
Das könnte Dich auch interessieren
Schmierung
Ohne Schmierung geht nichts: Jedes Lager läuft mit Fett- oder Ölschmierung, was die Grundvoraussetzung für die Vermeidung eines metallischen Kontakts der Lagerkomponenten, sprich von Wälzkörpern,




